2020-08-01

逐次代入法、Wegstein法

Python

はじめに

実際に使う機会は少ないと思われるが、基礎として知っておいた方がよいと思われる逐次代入法、Wegstein法について触れ、 Pythonで計算した例を示す。

逐次代入法

方程式を次の形にして、

$x = f(x)$

解の最初の予測値を右辺に代入して計算し、得られた値を第2の予測値として再び右辺に代入して計算、を繰り返し近似解を得る数値解法。新しい解と1つ前の解の差が予め決めた許容値を下回るまで計算を繰り返す。

例えば次の方程式の解を求める場合は（解は $x=1.25$ )、

$\displaystyle{ \frac{1}{x} = 0.8 }$

まず次の形に式変形し、

$\displaystyle{ x = \frac{1}{x} - 0.8 + x }$

例えば次の手順で解が求まる。

x1 = 2  # 最初の予測値
err = 1e10  # 計算終了判定用

while err > 1e-5:  # 計算終了判定
    x2 = 1.0/x1 - 0.8 + x1  # x = f(x)
    err = abs(x1 - x2)
    x1 = x2

print(x1)

Pythonコード実行すると次のとおり解が得られる。

1.250005085698445

Wegstein法

逐次代入法は $x=f(x)$ の中の $f(x)$ が次の条件でないと数値が収束しない。

$|f(x)'|<1$

これを解決する方法がWegstein法である。

例えば次の問題を考える。

$x^2 = 2$

逐次代入法で解ける形に式変形すると

$x = x^2 + x - 2$

$f(x)=x^2+x-2$ であり、その微分は $f(x)'=2x+1$ となり $|f(x)'|<1$ を多くの場合で満たさない。逐次代入法を試してみると、

x1 = 2

for i in range(5):
    x2 = x1**2 + x1 - 2
    x1 = x2
    print(x1)

結果は次の通り発散していく。

4
18
340
115938
13441735780

Wegstein法は最初の予測値から第2の予測値を求めるところまでは同じだが、第3以降の予測値は次式により算出する。

$x_{k+1} = t\times f(x_k) + (1-t)\times x_k \qquad (k=2, 3, \cdots)$

ここで、

$\displaystyle{ t = \frac{1}{1-s},\qquad s=\frac{f(x_k) - f(x_{k-1})}{x_k - x_{k-1}} }$

先程の問題 ( $x^2 = 2$ ) は次のように解ける。

def f(x):
    return x**2 + x - 2  # f(x)

x1 = 2  # 最初の予測値
x2 = f(x1)  # 第2の予測値
err = 1e10

while err > 1e-5:
    s = (f(x2) - f(x1))/(x2 - x1)
    t = 1.0/(1.0 - s)
    x3 = t * f(x2) + (1.0 - t) * x2
    err = abs(x3 - x2)
    x1 = x2
    x2 = x3

print(x2)

結果は下記。逐次代入法では発散したが、Wegstein法ではちゃんと収束する。なお初期値により＋−が変わる。

1.4142135625159447

参考

Wegstein法について、今は市販されていないようであるが、下記書籍で少し詳しく説明されている。

化学工学の基礎―化学プロセスとその計算 | A.L.マイヤーズ, W.D.サイダー, 大竹伝雄 |本 | 通販 | Amazon

2020-07-28

Pythonを用いた連立１次方程式の数値解法（LU分解）

Python

はじめに

Python (Numpy, Scipy) を用いて連立１次方程式を数値的に解く方法についてメモを記す。

例題

$\begin{aligned} &x+2y-z=2 \\ &2x-y-z=-3 \\ &5x+y-3z=-2 \end{aligned}$

これを行列で表すと、

$\mathbf{A}= \begin{bmatrix} 1 & 2 & -1 \\ 2 & -1 & -1 \\ 5 &1 &-3 \\ \end{bmatrix}, \quad \mathbf{x}= \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}, \quad \mathbf{b}= \begin{bmatrix} 2 \\ -3 \\ -2 \\ \end{bmatrix}$

$\mathbf{A} \mathbf{x} = \mathbf{b}$

解き方

numpy.linalg.solveを使って次のように計算できる。

import numpy

A = numpy.array([[1, 2, -1],
                 [2, -1, -1],
                 [5, 1, -3]])

b = numpy.array([2,
                 -3,
                 -2])

x = numpy.linalg.solve(A, b)

print x

結果は次のとおりとなる。

array([1., 2., 3.])

1組の連立方程式を単発で解く場合は上の方法で問題ないが、 $\textbf{A}$ の部分は変わらずに $\textbf{b}$ が変わる場合を数多く解く場合には次のLU分解を使うやり方のほうが計算時間を節約できる。一度計算して求めたlu_factorを使いまわして $\textbf{b}$ が変わった場合を計算すればよい。

import numpy
import scipy.linalg

A = numpy.array([[1, 2, -1],
                 [2, -1, -1],
                 [5, 1, -3]])

b = numpy.array([2,
                 -3,
                 -2])

lu = scipy.linalg.lu_factor(A)

x = scipy.linalg.lu_solve(lu, b)

2020-07-24

管型反応器のモデリングと数値計算

はじめに

シンプルな条件での管型反応器のモデリング・数値計算を行う。

管型反応器

下図のようなA→Bの反応を行う管型反応器において、初期は管型反応器内に成分A, Bが存在しない状態として、入口から成分Aを供給し始めたあとの反応器内のAの濃度変化を考える。反応熱は小さく等温反応であり、また流体の流れはプラグフローであり管半径方向の流量、濃度は一定であるものとする。

f:id:schemer1341:20200724002116p:plain:w350

物質収支

上図の微小区間⊿z [m]における成分Aの物質収支は次の関係で表される。

(Aの流入) - (Aの流出) + (反応によるAの生成) = (Aの蓄積)

Aの流量を $F_A$ [mol/s]、Aの反応速度を $r_A$ [mol/m3/s]、微小区間内の成分Aの物質量を $n_A$ [mol]として微小時間⊿t [s]における物質収支を数式で表すと下記となる。

$\displaystyle{ F_A|_z - F_A|_{z+\Delta z} + r_A \times S \times \Delta z = \frac{n_A|_{t+\Delta t} - n_A|_t}{\Delta t} }$

$S$ は反応管断面積 [m2] である。ここで両辺を $S\Delta z$ で割り、 $n_A/(S\Delta z)=c_A$ (濃度 [mol/m3])とすると、

$\displaystyle{ \frac{1}{S} \frac{F_A|_z - F_A|_{z+\Delta z}}{\Delta z} + r_A = \frac{c_A|_{t+\Delta t} - c_A|_t}{\Delta t} }$

$\Delta z \rightarrow 0$ 、 $\Delta t \rightarrow 0$ の極限を取ると

$\displaystyle{ -\frac{1}{S} \frac{\partial F_A}{\partial z} + r_A = \frac{\partial c_A}{\partial t} }$

ここで $F_A = vc_A$ ( $v$ は全流体流量 [m3/s])で表され、 $v$ は一定であると仮定し、空塔速度 $u=v/S$ [m/s]を用いると次式となる。

$\displaystyle{ -u \frac{\partial c_A}{\partial z} + r_A = \frac{\partial c_A}{\partial t} }$

反応速度

成分Aの反応速度は濃度に比例するとして次式で表す。

$\displaystyle{ -r_A=kc_A }$

$k$ は反応速度定数 [1/s]、成分Aは反応で消失するのでマイナスが付く。

初期・境界条件

初期は反応管内にAが存在しないのですべての位置で濃度ゼロ。境界条件は入口で供給されるAの濃度 $c_{A0}$ とする。

$\begin{aligned} c_A = 0 \quad &{\rm at} \quad t = 0 \\ c_A = c_{A0} \quad &{\rm at} \quad z = 0 \\ \end{aligned}$

以上で入口から成分Aを供給し始めたあとの反応器内のAの濃度変化を計算できる状態となった。

解析解

このままの形で解析解を得られるか定かでないが、長い時間が経過し定常状態に至った場合については簡単に解析解が得られる。定常状態では濃度の時間変化がないので蓄積を表す項 $\partial c_A/\partial t$ がゼロとなり、独立変数が z だけの常微分方程式になる。この条件では次の解析解が得られる。

$c_A = c_{A0}e^{-kz/u}$

数値解

まず方程式を整理して、

$\displaystyle{ \frac{\partial c_A}{\partial t} = -u\frac{\partial c_A}{\partial z} - kc_A }$

ここで位置 $z$ と時刻 $t$ を次の形で表すこととし( $i$ 、 $j$ は整数)、

$z_i = i \times \Delta z, \quad t_j = j \times \Delta t$

濃度 $c_A$ について次の表記の仕方をすることとする( $A$ は見づらくなるので省略)。

$c_{i, j} = f(z_i, t_j)$

偏微分を次の通り位置について後退差分、時間について前進差分で近似する。

$\begin{aligned} \frac{\partial c_A}{\partial z} &\fallingdotseq \frac{c_{i,j} - c_{i-1,j}}{\Delta z} \\ \frac{\partial c_A}{\partial t} &\fallingdotseq \frac{c_{i, j+1} - c_{i, j}}{\Delta t} \\ \end{aligned}$

また、項 $kc_A$ の $c_A$ は次の通り位置方向の2点の平均で近似する。

$\displaystyle{ c_A \fallingdotseq \frac{c_{i, j} + c_{i-1, j}}{2} }$

これら近似式を微分方程式に代入し整理すると下記の形となり、濃度 $c$ の値を時刻0から順次計算していくことができる。

$\displaystyle{ c_{i, j+1} = c_{i, j} - \frac{u \Delta t}{\Delta z} (c_{i, j} - c_{i-1, j}) - \frac{k \Delta t}{2}(c_{i, j} + c_{i-1, j}) }$

算出イメージは下図のようになる。横軸を $i$ (位置方向)、縦軸を $j$ (時間方向)とした格子であり、各格子点がある位置、ある時刻での濃度を表している。濃度既知の格子点は青色、濃度未知は赤色であるが、緑矢印の方向に値が求まるイメージとなる。位置について後退差分を取ったが、前進差分にすると出口(一番右の格子点)の計算ができない。

f:id:schemer1341:20200724003136p:plain:w450

流体流れの風上側の値から次の値を算出しており、いわゆる「風上差分法」と呼ばれる計算スキームに該当する。位置、時間の差分の取り方によってFTCSスキームとかクランク・ニコルソン法とか名前がついているが、差分式だけで考えるのでなく図も描いて考えるとイメージをつかみやすい。

計算

Pythonを用いて計算した。ソースコードは下記リンク先にある。

cemodeling/simple_tube_reactor.py at master · nakamura-13/cemodeling · GitHub

反応管の全長は1.0 m、供給流体の空塔速度は0.1 m/s、成分Aの入口濃度は1.0 mol/m3とした。反応速度定数は0.4 1/s とした。成分Aの初期濃度は反応管全体でゼロとした。位置方向の分割数は50とし(格子点数は51点)、時刻のステップ幅は0.1秒とした。

計算結果を下グラフに示す。横軸は位置、縦軸は濃度であり、時刻0.5秒、2秒、4秒、10秒の濃度の分布を示している。供給流体が反応管を抜けきる10秒後には定常状態に至っており、その濃度分布は解析解と一致していることが確認できる。

f:id:schemer1341:20200724003754p:plain:w500

2020-07-16

1次元非定常熱伝導の数値計算

はじめに

前回、1次元非定常熱伝導のモデリングを行い偏微分方程式を導いたが、今回は数値計算によりその解を得る。

方程式

加温したステンレス棒を急に冷水につける問題について、前回導いた偏微分方程式および初期・境界条件は下記のとおりである。

$\displaystyle{ \frac{\partial T}{\partial t} = \alpha \Bigl( \frac{\partial^2 T}{\partial r^2} + \frac{1}{r} \frac{\partial T}{\partial r} \Bigr) }$

$\begin{aligned} T = T_0 \quad &{\rm at} \quad t = 0 \\ T = T_1 \quad &{\rm at} \quad r = R \\ \frac{\partial T}{\partial r} = 0 \quad &{\rm at} \quad r = 0 \end{aligned}$

差分近似による数値解法

微小距離を $\Delta r$ 、微小時間を $\Delta t$ とおき、位置 $r$ と時刻 $t$ を次の形で表すこととする。

$r_i = i \times \Delta r, \quad t_j = j \times \Delta t$

ここで $i$ 、 $j$ は整数とする。温度 $T$ は位置 $r$ と時刻 $t$ の関数であるが、次の記載の仕方をすることとする。

$T_{i, j} = f(r_i, t_j)$

このとき偏微分の差分による近似式は次の形で表される。

$\begin{aligned} \frac{\partial T}{\partial t} &\fallingdotseq \frac{T_{i, j+1} - T_{i, j}}{\Delta t} \\ \frac{\partial T}{\partial r} &\fallingdotseq \frac{T_{i+1, j} - T_{i, j}}{\Delta r} \\ \frac{\partial^2 T}{\partial r^2} &\fallingdotseq \frac{T_{i+1, j} -2T_{i, j} + T_{i-1, j}}{(\Delta r)^2} \end{aligned}$

3つ目については、次の形で近似していると考えれば導くことができる。

$\displaystyle{ \frac{\partial^2 T}{\partial r^2} \fallingdotseq \frac{(\partial T/\partial r)_{i, j} - (\partial T/\partial r)_{i-1, j} }{\Delta r} }$

これら差分近似式を微分方程式に代入して整理すると次の形となる。この式から $T$ の値を順次算出していくことができる。

$\displaystyle{ T_{i, j+1} = T_{i, j} + \alpha \Bigl( \frac{T_{i+1, j} -2T_{i, j} + T_{i-1, j}}{(\Delta r)^2} + \frac{1}{r} \frac{T_{i+1, j} - T_{i, j}}{\Delta r} \Bigr) \Delta t }$

算出イメージ

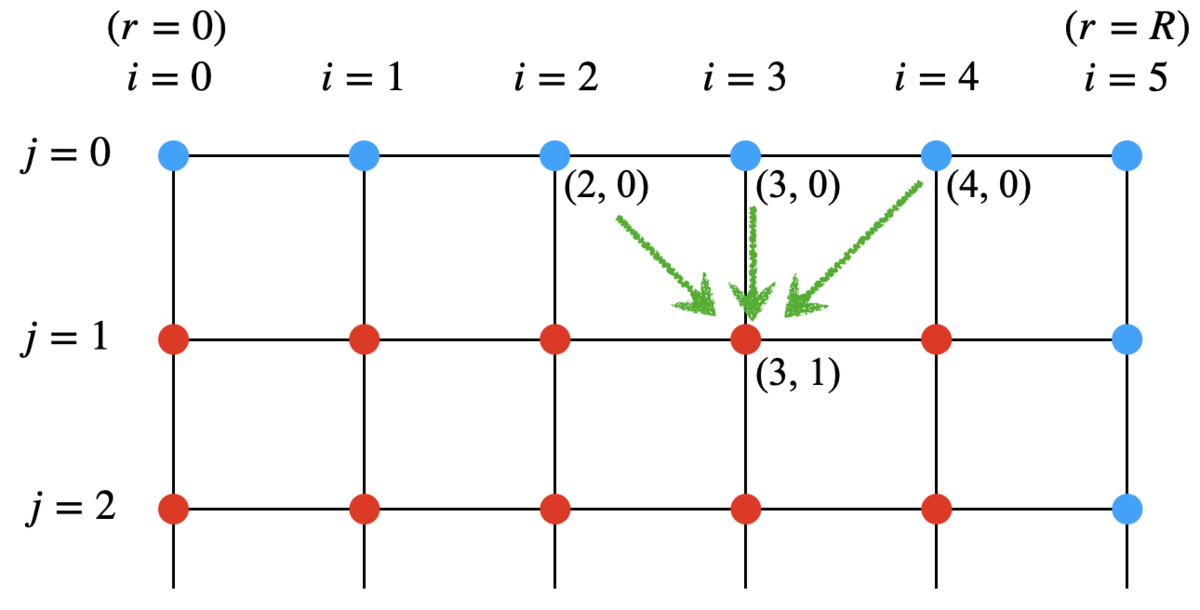
上の式を下図のイメージで捉えてみる。下図は横軸を $i$ (位置方向)、縦軸を $j$ (時間方向)とした格子であり、各格子点がある位置、ある時刻での温度を表している。一番上の行は $j=0$ における各位置の温度、すなわち初期条件を表しており、それぞれの温度は既知となる(既知の格子点は青色としている)。なお一番右の点は $r=R$ の温度であり、境界条件により初期以外のすべての時刻の値が既知となる。

上の式は、位置 $i$ における次の時刻の温度が、現時刻の位置 $i$ とその前後の位置の温度から求まるという形になっている。下図で言うと緑矢印の方向に値が求まるイメージである。時刻ゼロの温度から次の時刻の温度をすべて求め、それが済んだら時刻を進めて、さらに次の時刻の温度を求める、というふうに順次温度を求めていくことができる。

f:id:schemer1341:20200715000140p:plain:w500

計算

Pythonを用いて計算した。ソースコードは下記リンク先にある。

cemodeling/conduction_1d_unsteady.py at master · nakamura-13/cemodeling · GitHub

ステンレス棒の初期温度は50℃で全体が均一とし、冷水温度は0 ℃とした。ステンレス棒の半径は1.5 cmである。位置(半径)方向の分割数は10とし(よって格子点数は11点)、時刻のステップ幅は0.1秒とした。ステンレス棒の密度、熱伝導率、比熱容量はSUS304の値を参考に決めた（具体的な値はソースコード参照）。

計算結果を下グラフに示す。横軸は半径方向位置、縦軸は温度であり、時刻0秒、5秒、10秒、20秒、40秒の温度の分布を示している。40秒後にはステンレス棒の芯までほぼ冷水温度の0℃まで低下していることがわかる。

f:id:schemer1341:20200716002841p:plain:w500

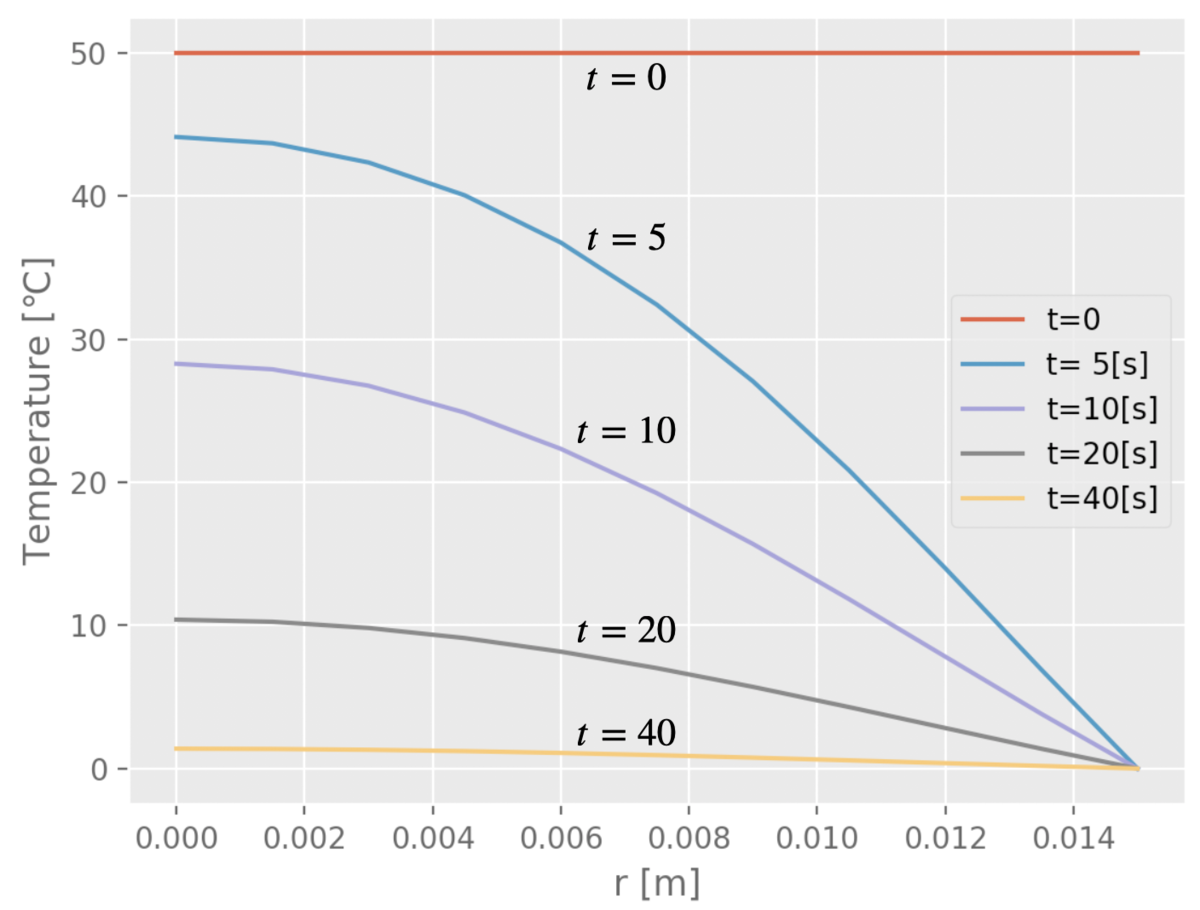
なお、下記書籍のChapter 12にある1次元非定常熱伝導の解析解グラフを参照して本問題の解析解を確認してみると、棒の芯の温度は10秒で28℃、20秒で10℃ほどになり、数値計算の結果と矛盾がないことを確認できる。

Amazon | Transport Phenomena | Bird, R. Byron, Stewart, Warren E., Lightfoot, Edwin N. | Dynamics

その他の参考書籍

Cによる数値計算法入門(第2版)新装版 | 堀之内總一, 酒井幸吉, 榎園茂 |本 | 通販 | Amazon

2020-07-11

1次元非定常熱伝導のモデリング

はじめに

円柱の１次元非定常熱伝導のモデリングを行う。（数値計算は別途）

円柱の1次元非定常熱伝導

円柱状のステンレス棒を均一に加温し、それを突如冷水の水槽に入れたときのステンレス棒の温度変化を考える。

熱収支

下に模式図を示す。棒はかなり長く、棒の両端の面からの熱の伝わりは無視できるものとする。

f:id:schemer1341:20200711150412p:plain:w300

このとき棒から長さ $L$ [m]の円柱を取り出し、その半径 $r$ [m]から半径 $r+\Delta r$ [m]のリング状の領域(灰色部分)の熱収支は次の関係で表される。

(リング内側からの入熱) − (リング外側への出熱) ＝ (リング内の熱の蓄積)

熱流束を $q$ [J/m2/s]、温度を $T$ [℃]として微小時間 $\Delta t$ [s] における熱収支を数式で表すと以下の形となる。

$q|_r (2\pi r L)\Delta t - q|_{r+\Delta r} \{2\pi (r+\Delta r) L\}\Delta t = (\rho C_p) (T|_{t+\Delta t} - T|_t) (2 \pi r L \Delta r)$

ここで $\rho$ はステンレス棒の密度 [kg/m3]、 $C_p$ はステンレス棒の比熱容量 [J/kg/℃]である。これを式変形していくと次の形に整理できる。

$\displaystyle{-\rho C_p \frac{T|_{t+\Delta t} - T|_t}{\Delta t} = \frac{q|_{r+\Delta r} - q|_r}{\Delta r} + \frac{1}{r}q|_{r+\Delta r}}$

$\Delta t \rightarrow 0$ 、 $\Delta r \rightarrow 0$ の極限を取ると次式となる。

$\displaystyle{ - \rho C_p \frac{\partial T}{\partial t} = \frac{\partial q}{\partial r} + \frac{1}{r}q }$

熱伝導の速度

熱流束 $q$ は次のフーリエの法則から表現されるものとする。

$\displaystyle{ q = - k \frac{\partial T}{\partial r} }$

$k$ は熱伝導率 [W/m/K] ([J/s/m/℃]と見てもよい)である。これを上の熱収支式に代入し、熱拡散率 $\alpha = k/(\rho C_p)$ とおくと、

$\displaystyle{ \frac{\partial T}{\partial t} = \alpha \Bigl( \frac{\partial^2 T}{\partial r^2} + \frac{1}{r} \frac{\partial T}{\partial r} \Bigr) }$

が得られる。初期条件、境界条件が決まれば温度 $T$ について方程式が解ける。

初期条件、境界条件

均一に温まった棒を急に冷水につける状況を考え、棒の表面は瞬間的に冷水温度になり、棒の中心の熱流束はゼロと考えると、初期条件、境界条件は以下の通りとなる。

$\begin{aligned} T = T_0 \quad &{\rm at} \quad t = 0 \\ T = T_1 \quad &{\rm at} \quad r = R \\ \frac{\partial T}{\partial r} = 0 \quad &{\rm at} \quad r = 0 \end{aligned}$

$T_0$ はステンレス棒の初期温度、 $T_1$ は冷水の温度、 $R$ はステンレス棒の半径で $r=R$ は棒の表面位置を示す。

解析解

この問題の解析解は、筆者には解けないので触れないが、知りたい方は下記書籍のChapter 12を参照されると良い。

Amazon | Transport Phenomena | Bird, R. Byron, Stewart, Warren E., Lightfoot, Edwin N. | Dynamics

和書なら、解き方は書いてないものの、解の説明が下記書籍の第5章に載っている。

道具としての微分方程式偏微分編式をつくり、解いて、「使える」ようになる (ブルーバックス) | 斎藤恭一 |本 | 通販 | Amazon

おわりに

円柱の1次元非定常熱伝導について偏微分方程式を導いた。次回はこの問題の数値計算に取り組み予定。

2020-07-10

バッチ反応のモデリングと数値計算

はじめに

バッチ反応(液相、一次反応)の非常に簡単な例でモデリング、数値計算を行う。

モデリング

下図に示すとおり成分Aから成分Bを生じる液相バッチ反応について、時刻tにおける成分Aの量を求めることを考える。

f:id:schemer1341:20200709232018p:plain:w300

物質収支

(成分A物質量の変化速度) = (成分Aの反応速度)であり、時刻をt [s]として次式で表される。

$\displaystyle{\frac{dn_A}{dt}=r_AV}$

両辺を定数である体積Vで割り、 $n_A/V=c_A$ (濃度)とすると

$\displaystyle{\frac{dc_A}{dt}=r_A}$

反応速度

成分Aの反応速度は成分Aの濃度の１次に比例とすると、反応速度定数を $k$ [1/s]として次式で表される。

$-r_A = kc_A$

(Aは消失するのでマイナスが付く)

解析解

物質収支と反応速度から次の形となる。

$\displaystyle{\frac{dc_A}{dt}=-kc_A}$

ここで初期条件を $c_A=c_{A0}$ at $t=0$ として方程式を解くと $c_A$ と $t$ の関係が求まる。

$\begin{aligned} \frac{1}{c_A}dc_A &= -kdt \\ \int^{c_A}_{c_{A0}}\frac{1}{c_A}dc_A &= -k\int^{t}_{0}dt \\ \ln \frac{c_A}{c_{A0}} &= -kt \\ c_A &= c_{A0} e^{-kt} \end{aligned}$

数値解

オイラー法を用いると時刻 $t$ における $c_A|_t$ とその微小時間 $\Delta t$ 後の $c_A|_{t+\Delta t}$ は次式で関連付けられる。

$\displaystyle{c_A|_{t+\Delta t} = c_A|_t + \frac{dc_A|_t}{dt} \Delta t}$

微分部分を代入すると、

$\displaystyle{c_A|_{t+\Delta t} = c_A|_t - k c_A|_t \Delta t}$

具体的な微小時間値を決めたら初期条件から順次数値を計算していけばよい。

解析解と数値解の比較

Pythonを用いて計算した。ソースコードは下記リンク先にある。
cemodeling/batch_reaction.py at master · nakamura-13/cemodeling · GitHub

初期濃度 $c_{A0}=1$ [mol/m3]、反応速度定数 $k=0.01$ [1/s]、微小時間を30秒として計算した結果を下グラフに示す。横軸は時刻、縦軸は濃度である。600秒くらいで成分Aは反応してほぼ無くなる。青い線が数値解である。

f:id:schemer1341:20200710223918p:plain:w500

微小時間を1秒にすると、解析解と数値解はほぼ一致する。

f:id:schemer1341:20200710223957p:plain:w500

おわりに

ここでは常微分方程式の問題を取り扱ったが、次回は偏微分方程式の問題に取り組み予定。

2020-07-06

鉛直投げ上げの数値解法

はじめに

高校物理で最初の方に習う物体の鉛直投げ上げをオイラー法で解く方法について記す。数値計算を使わなくても簡単に解ける問題であるが、数値計算の超基本的な考え方を確認するにはよいと思われる。解析解と数値解法を示し、解析解と数値解を比較してみる。

鉛直投げ上げの解析解

位置をz [m]、時刻をt[秒]とし、物体を鉛直（真上）に初速度 $v_0$ [m/s]で投げ上げたときの時刻tにおける物体の位置zを知りたいとする。重力による物体にかかる加速度は $-g$ [m/s $^2$ ]とする（真上方向を正として）。物体へかかる空気抵抗は無視するとして、物体の位置の時刻の関係は次の微分方程式で表される。

f:id:schemer1341:20200705214627p:plain:h50

これは変数分離形の微分方程式であり、初期条件を下記として、

f:id:schemer1341:20200705214928p:plain:h24

次のように解ける。

f:id:schemer1341:20200705222113p:plain:h55

f:id:schemer1341:20200705222137p:plain:h55

f:id:schemer1341:20200705222159p:plain:h55

これが時刻tにおける物体の位置zを表す解析解である。高校物理ではこの式が脈絡なく出てくるため、高校生の時はかなり混乱したものです。

数値解

オイラー法

雑に説明すれば、時刻tから僅かな時間が経過した時刻 $t+\Delta t$ の位置zを予想するのに、本来 $dz/dt$ の値は時刻tに従い連続的に変化するが微小時間 $\Delta t$ の間だけは一定値とみなして位置zの近似解を得る方法である。具体的には以下の通りにして時刻 $t+\Delta t$ と時刻 $t$ の位置zを関係付ける。

f:id:schemer1341:20200705231357p:plain:h55

なお、これは式変形すれば下記の形となり、 $\Delta t\rightarrow 0$ の極限を取れば微分の定義そのものである。

f:id:schemer1341:20200705232003p:plain:h55

初期(時刻 $t=0$ )の位置z(0)がわかっていれば、それを用いて $\Delta t$ 経過後の位置z(0+ $\Delta t$ )を算出し、さらにそれから $\Delta t$ 経過後の位置z(0+ $2\Delta t$ )を算出する、という形で順に位置zの近似値を計算していくことができる。

解析解と数値解の比較

Pythonを用いて計算した。ソースコードは下記リンク先にある。

cemodeling/vertical_throw.ipynb at master · nakamura-13/cemodeling · GitHub

初期速度 $v_0=20$ [m/s]、重力加速度 $g=9.8$ [m/s2]、微小時間を0.1秒として計算した結果を下グラフに示す。横軸は時刻、縦軸は位置である。約4秒後に位置z=0に戻ってくる計算結果となる。青い線が数値解であるが、あくまで近似であるため微妙にずれが生じている。

微小時間を短くすれば解析解に近づく。下図は微小時間を0.01秒にした結果だが、数値解はほぼ解析解に一致している。微小時間を小さくしているため精度が改善する一方で、計算量は増加する。

終わりに

非常に簡単な問題について数値解法を適用したが、より現実的で複雑な問題（大体は連立偏微分方程式）においても基本は同じなので、超基本的な考え方を知る上では役に立つと思う。