2021-01-23

管内流れの1次元移流拡散方程式

Python

はじめに

管内の移流・拡散を対象として次の移流拡散方程式を導出し、数値計算する。

$\displaystyle{ \frac{\partial c}{\partial t} = -u \frac{\partial c}{\partial x} + D \frac{\partial^2 c}{\partial x^2} }$

導出

以前の記事で導いた移流方程式および拡散方程式を組み合わせればよい。

移流方程式:

$\displaystyle{ \frac{\partial c}{\partial t} = - u \frac{\partial c}{\partial x} }$

拡散方程式:

$\displaystyle{ \frac{\partial c}{\partial t} = D \frac{\partial^2 c}{\partial x^2} }$

移流拡散方程式:

$\displaystyle{ \frac{\partial c}{\partial t} = - u \frac{\partial c}{\partial x} + D \frac{\partial^2 c}{\partial x^2} }$

差分近似による数値解法

まず微小距離を $\Delta x$ 、微小時間を $\Delta t$ とし、位置 $x$ と時刻 $t$ を次の形で表すこととする。

$x_i = i \times \Delta x, \quad t_j = j \times \Delta t$

ここで $i$ 、 $j$ は整数とする。濃度 $c$ は位置 $x$ と時刻 $t$ の関数であるが、 $c_{i, j}$ は次を意味するものとする。

$c_{i, j} = f(x_i, t_j) = f(i\Delta x, j\Delta t)$

このとき偏微分の差分法による近似式は次の形で表される。

$\begin{aligned} \frac{\partial c}{\partial t} &\fallingdotseq \frac{c_{i, j+1} - c_{i, j}}{\Delta t} \\ \frac{\partial c}{\partial x} &\fallingdotseq \frac{c_{i+1, j} - c_{i, j}}{\Delta x} \\ \frac{\partial^2 c}{\partial x^2} &\fallingdotseq \frac{c_{i+1, j} -2c_{i, j} + c_{i-1, j}}{(\Delta x)^2} \end{aligned}$

これら近似式を1次元移流拡散方程式に代入して整理すると次の形となる。この式および初期・境界条件から $c$ の値を順次算出していくことができる。

$\displaystyle{ c_{i, j+1} = c_{i, j} - \frac{(\Delta t) u}{\Delta x} (c_{i+1,j} - c_{i,j}) + \frac{(\Delta t) D}{(\Delta x)^2} (c_{i+1, j} - 2 c_{i, j} + c_{i-1, j}) }$

計算例

管長さを0.1 m、空塔速度 $u$ を $4\times 10^{-5}$ m/s、拡散係数 $D$ を $1\times 10^{-7}$ m2/sとし、初期・境界条件を以下とする。

初期条件:

$\displaystyle{ c = 0 \quad at \quad x \lt 0.02,\ 0.025 \lt x \\ c = 1 \quad at \quad 0.02 \leqq x \leqq 0.025 }$

境界条件:

$\displaystyle{ c = 0 \quad at \quad x = 0,\ x = 0.1 }$

Pythonを用いて計算した (ソースコード)。結果は下記グラフとなる (時間の単位は秒)。濃度分布が左右に広がりながら、かつ分布の中心が右に動いていく様子が見て取れる。

f:id:schemer1341:20210123230140p:plain:w450

2020-12-21

管内の1次元拡散方程式

Python

はじめに

管内の拡散を対象として次の拡散方程式を導出し、数値計算する。

$\displaystyle{ \frac{\partial c}{\partial t} = D \frac{\partial^2 c}{\partial x^2} }$

導出

f:id:schemer1341:20201219203616p:plain:w300

管内に液体が満たされていて、その中に溶解した物質が左から右へ拡散しているとする。液体中のある成分Aについて、微小区間 $\Delta x$ における微小時間 $\Delta t$ の間の物質収支は、

(拡散による微小区間へのAの流入量) - (拡散による微小区間からのAの流出量) = (微小区間内のAの蓄積量)

と考えられる。ここでAの質量流束を $j$ [kg/m2/s]、微小区間内の成分Aの濃度を $c$ [kg/m3]として物質収支を数式で表すと下記となる（流束は管の半径方向に対し一定と考える)。

$\displaystyle{ j_x \times S \times \Delta t - j_{x+\Delta x} \times S \times \Delta t = c_{t+\Delta t} \times S \times \Delta x - c_t \times S \times \Delta x }$

両辺を $S \Delta x \Delta t$ で割ると、

$\displaystyle{ \frac{j_x - j_{x+\Delta x}}{\Delta x} = \frac{c_{t+\Delta t} - c_t }{\Delta t} }$

$\Delta x \rightarrow 0, \quad \Delta t \rightarrow 0$ の極限を取ると、

$\displaystyle{ -\frac{\partial j}{\partial x} = \frac{\partial c}{\partial t} }$

ここで、フィックの法則より、

$\displaystyle{ j = - D \frac{\partial c}{\partial x} }$

これを上の式に代入すると、次の1次元拡散方程式が得られる( $D$ は拡散係数 [m2/s]で、ここでは一定値で不変とする)。

$\displaystyle{ \frac{\partial c}{\partial t}=D \frac{\partial^2 c}{\partial x^2} }$

差分近似による数値解法

まず微小距離を $\Delta x$ 、微小時間を $\Delta t$ とし、位置 $x$ と時刻 $t$ を次の形で表すこととする。

$x_i = i \times \Delta x, \quad t_j = j \times \Delta t$

ここで $i$ 、 $j$ は整数とする。濃度 $c$ は位置 $x$ と時刻 $t$ の関数であるが、 $c_{i, j}$ は次を意味するものとする。

$c_{i, j} = f(x_i, t_j) = f(i\Delta x, j\Delta t)$

このとき偏微分の差分法による近似式は次の形で表される。

$\begin{aligned} \frac{\partial c}{\partial t} &\fallingdotseq \frac{c_{i, j+1} - c_{i, j}}{\Delta t} \\ \frac{\partial^2 c}{\partial x^2} &\fallingdotseq \frac{c_{i+1, j} -2c_{i, j} + c_{i-1, j}}{(\Delta x)^2} \end{aligned}$

これら近似式を1次元拡散方程式に代入して整理すると次の形となる。この式および初期・境界条件から $c$ の値を順次算出していくことができる。

$\displaystyle{ c_{i, j+1} = c_{i, j} + \frac{(\Delta t) D}{(\Delta x)^2} (c_{i+1, j} - 2 c_{i, j} + c_{i-1, j}) }$

計算例

管長さを0.1 m、拡散係数 $D$ を $10^{-7}$ m2/s とし、初期・境界条件を以下とする。

初期条件:

$\displaystyle{ c = 0 \quad at \quad x \lt 0.04,\ 0.06 \lt x \\ c = 1 \quad at \quad 0.04 \leqq x \leqq 0.06 }$

境界条件:

$\displaystyle{ c = 0 \quad at \quad x = 0,\ x = 0.1 }$

Pythonを用いて計算した (ソースコード)。結果は下記グラフとなる (時間の単位は秒)。濃度分布が左右に広がっていく様子が見て取れる。

f:id:schemer1341:20201221002020p:plain:w400

2020-12-15

管内流れの1次元移流方程式

はじめに

管内の流れを対象として次の1次元移流方程式を導出する。

$\displaystyle{ \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} = 0 }$

導出

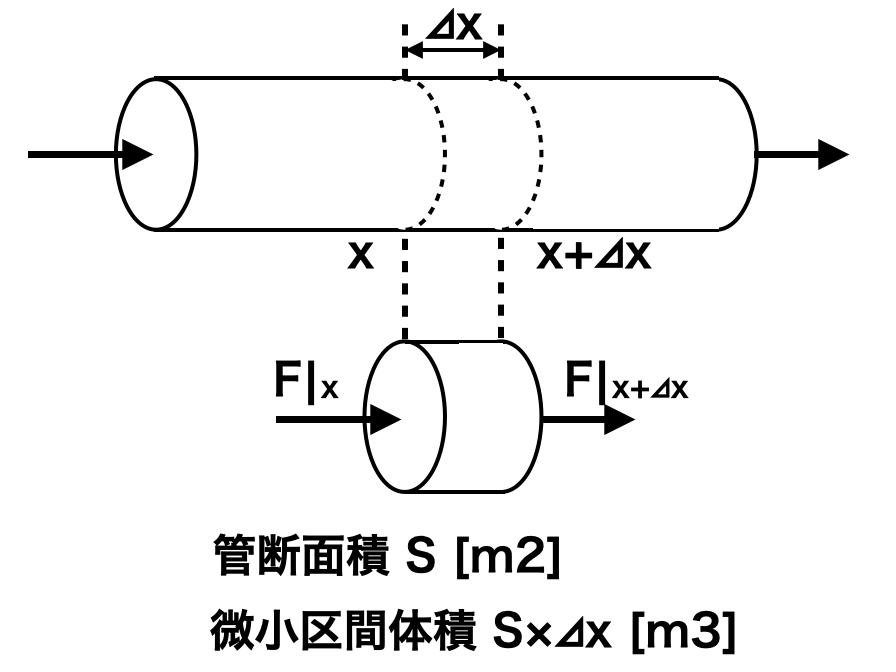
f:id:schemer1341:20201213234523p:plain:w300

気体混合物が図の管内を左から右へ流れているとする。気体混合物中のある成分Aについて、微小区間 $\Delta x$ における微小時間 $\Delta t$ の間の物質収支は、

(微小区間へのAの流入量) - (微小区間からのAの流出量) = (微小区間内のAの蓄積量)

と考えられる。ここでAの流量を $F$ [kg/s]、微小区間内の成分Aの量を $m$ [kg]として物質収支を数式で表すと下記となる（流量は管の半径方向に対し一定と考える)。

$\displaystyle{ F|_x \times \Delta t - F|_{x+\Delta x} \times \Delta t = m|_{t+\Delta t} - m|_t }$

両辺を $\Delta t$ および微小区間体積 $S \Delta x$ で割ると、

$\displaystyle{ \frac{1}{S} \frac{F|_x - F|_{x+\Delta x}}{\Delta x} = \frac{m|_{t+\Delta t}/(S\Delta x) - m|_t /(S\Delta x)}{\Delta t} }$

流量 $F$ を全ガス流量 $v$ [m3/s] と濃度 $c$ [kg/m3] の積 ( $vc$ ) に置き換え、また $m/(S\Delta x)$ は濃度 $c$ と等しいことを考慮すると上式は次式の通りに書き直せる。

$\displaystyle{ \frac{v}{S} \frac{c|_x - c|_{x+\Delta x}}{\Delta x} = \frac{c|_{t+\Delta t} - c|_t}{\Delta t} }$

空塔速度 $u=v/S$ [m/s]とし、 $\Delta x \rightarrow 0, \ \Delta t \rightarrow 0$ の極限をとると、

$\displaystyle{ -u \frac{\partial c}{\partial x} = \frac{\partial c}{\partial t} }$

式を整理すると下記となる。

$\displaystyle{ \frac{\partial c}{\partial t} + u \frac{\partial c}{\partial x} =0 }$

一次元移流方程式は初期の濃度の分布が速度uでその分布の形のまま運ばれていく様子を表す。この式単独で使うことはなく、拡散や反応など他の現象と組み合わせて使う。なおこの式を解いてもあまり実用性はないが、数値計算で解くのは非常にきびしい。解のイメージは下記が参考になる。

移流方程式の数値計算と可視化

2020-12-13

吸着平衡　ー平衡到達時の吸着量計算ー

Python

はじめに

下図のように気体(例えばCO2)を吸着する吸着材(例えばゼオライト)が容器に充填されていて、その中にCO2を封入したところ、気相中のCO2は徐々にゼオライトに吸着されていって最終的には平衡状態に至った。

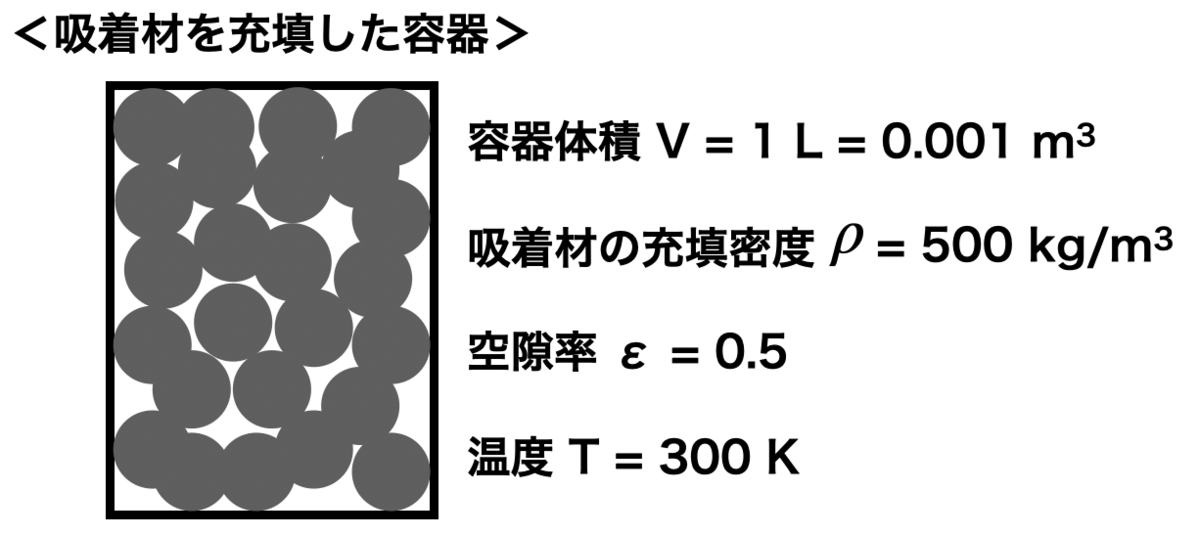
f:id:schemer1341:20201213200012p:plain:w400

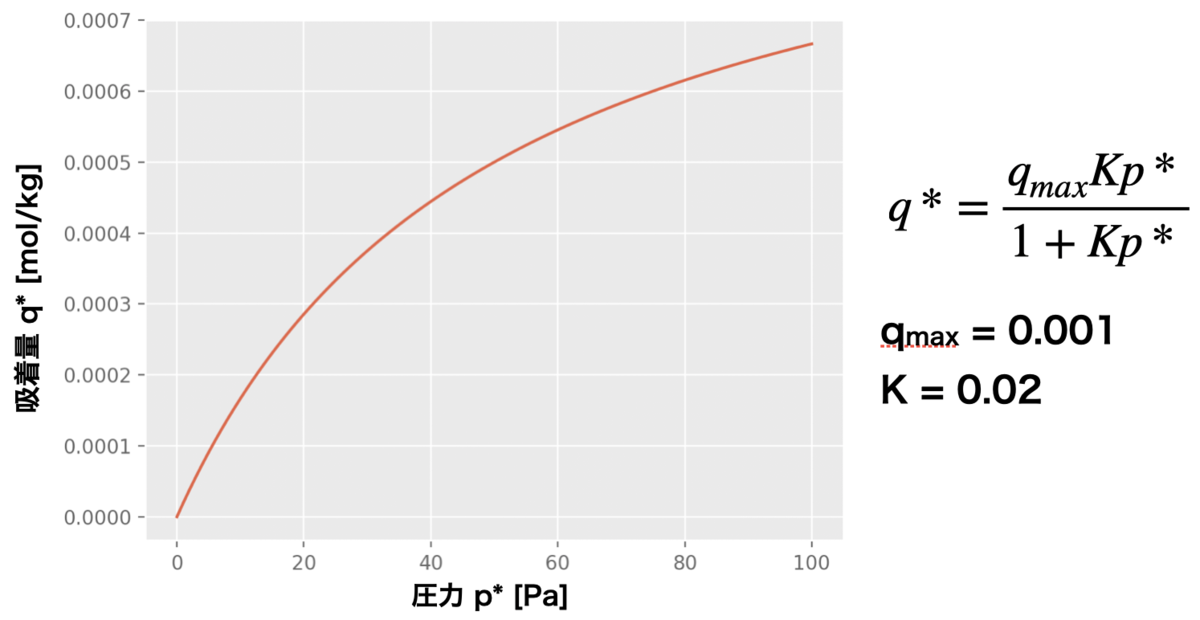
初期のCO2分圧が 50 Pa 、吸着量はゼロであったとして、平衡到達時のCO2分圧 [Pa]、CO2比吸着量 [mol/kg] (吸着材重量あたり吸着量)はいくらになるか。なお、CO2-ゼオライトの間の吸着平衡関係は下記のラングミュア式に従うものとする。

f:id:schemer1341:20201213201025p:plain:w500

解き方

初期と平衡到達後の気相・吸着材中の物質量合計は変わらないため物質量保存の式と、吸着平衡の式を同時に満たすCO2分圧、CO2比吸着量を求めればよい。

物質量保存の式は下記で表される。

(平衡時気相CO2量 mol) + (平衡時 CO2吸着量 mol) = (初期気相CO2量 mol) + (初期 CO2吸着量 mol)

$\displaystyle{ \frac{p^*\epsilon V}{RT}+\rho V q^* = \frac{p_0 \epsilon V}{RT} + \rho V q_0 }$

ここで $p^*,\ q^*$ は平衡時の分圧、吸着量、 $p_0,\ q_0$ は初期の分圧、吸着量である。気相CO2量はCO2が理想気体であるとして気体の状態方程式から求めている。

式を整理すると、

$\displaystyle{ \frac{\epsilon}{RT}(p^* - p_0) + \rho (q^* - q_0)=0 \quad \cdots \quad \text{(1)} }$

となる。これに次の吸着平衡式 (2) を代入すれば未知数は $p^*$ のみとなるので方程式を解くことができる。

$\displaystyle{ q^* = \frac{q_{max} K p^*}{1 + K p^*} \quad \cdots \quad \text{(2)} }$

とはいえ、手計算だとだいぶ面倒そうな形になるためPythonを用いて数値計算すると、

import scipy.optimize

R = 8.3145  # 気体定数 [J/K/mol]
Rho = 500  # 充填密度 [kg/m3]
Eps = 0.5  # 空隙率 [-]
T = 300  # 温度 [K]

def langmuir(p):
    qmax = 1e-3
    k = 2e-2
    return qmax * k * p / (1 + k * p)

def equation(p):
    p0 = 50  # 初期気相分圧 [Pa]
    q0 = 0  # 初期吸着量 [mol/kg]
    return Eps/R/T * (p - p0) + Rho * (langmuir(p) - q0)

print(scipy.optimize.newton(equation, 50))

1.0018627181806559

平衡時気相CO2分圧として約 $1.0$ Paが得られ、これを式(2)に代入すれば平衡時CO2比吸着量として約 $2.0\times10^{-5}$ mol/kg が求まる。

吸着平衡式の曲がりの癖が強い場合などにNewton法でうまく収束しないケースもあるかもしれない。その場合は計算初期値を変えたり、他の計算法に変える(ex. 二分法)ことを考える必要がある。

2020-12-13

Pythonを用いた非線形方程式の数値解法　ニュートン法

Python

はじめに

非線形方程式の数値解を得るためのニュートン法について、考え方とPythonを用いた計算のやり方を簡単に記す。

ニュートン法

次の非線形方程式を満たす $x$ を考える

$\displaystyle{ 2x^2 + x - 5 = 0 }$

上記方程式の左辺を $f(x)$ とおき、最初の近似解を $x_0$ としたとき、

$\displaystyle{ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}, \qquad x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} }$

と、順次計算していく方法。一般化すると下記。

$\displaystyle{ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} }$

適当なところで計算を終了する条件の設定が必要。

Pythonで計算するなら scipy.optimize.newton を使うのが楽。

import scipy.optimize

fx = lambda x: 2*x**2 + x - 5

print(scipy.optimize.newton(fx, 2))

> 1.3507810593582126

自分で関数を作るなら、たとえば $f'(x)$ を得るのに数値微分を使って次のやり方がある。

# 数値微分(中心差分)
def dfx(fx, x):
    h = 1e-8
    return (fx(x+h) - fx(x-h))/(2*h)

def newton(fx, x0):
    x1 = x0 - fx(x0)/dfx(fx, x0)
    if abs(x0 - x1) < 1e-5:
        return x1
    else:
        return newton(fx, x1)

print(newton(fx, 2))

> 1.3507810593595635

2020-08-09

Pythonを用いた連立１次方程式の数値解法（ガウス・ザイデル法）

Python

はじめに

連立1次方程式の数値解を得るためのガウス・ザイデル法について、考え方とPythonを用いた計算のやり方を簡単に記す。

ガウス・ザイデル法

次の連立方程式を考える。

$\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \end{bmatrix}$

以前に触れたヤコビ法は次の近似式を用い、解の最初の予測値を右辺に代入して $x_1, x_2, x_3$ を算出し、得られた値を第2の予測値として再び右辺に代入して計算、を繰り返し近似解を得る方法であった。

$\begin{aligned} x_1^{(k+1)} &= \frac{1}{a_{1,1}}(b_1 - a_{1,2}x_2^{(k)} - a_{1, 3}x_3^{(k)}) \\ x_2^{(k+1)} &= \frac{1}{a_{2,2}}(b_2 - a_{2,1}x_1^{(k)} - a_{2, 3}x_3^{(k)}) \\ x_3^{(k+1)} &= \frac{1}{a_{3,3}}(b_3 - a_{3,1}x_1^{(k)} - a_{3, 2}x_2^{(k)}) \\ \end{aligned}$

ガウス・ザイデル法はすでに求まった $x$ についてはその場ですぐに使用する。式で書くと次のようになる。1番目の式で求まった $x_1$ は2番目の式で使用し、1, 2番目の式で求まった $x_1, x_2$ は両方とも3番目の式で使用する。

f:id:schemer1341:20200809000829p:plain:w250

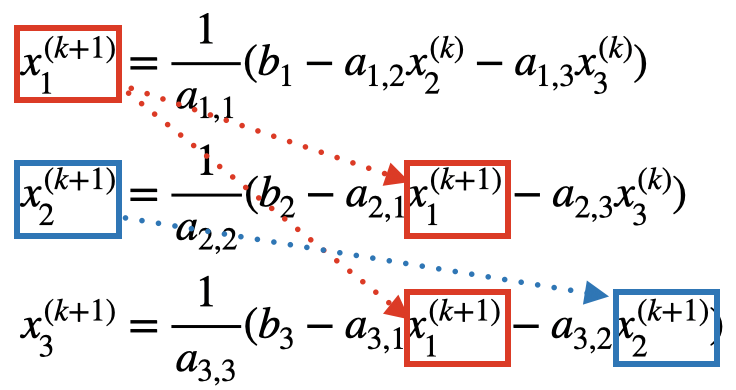
これら近似式は次のとおり行列の形で比較的簡単に表せる。まずはじめの方程式は

$\mathbf{A}= \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \\ \end{bmatrix}, \qquad \mathbf{x}= \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix}, \qquad \mathbf{b}= \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \end{bmatrix}$

として、

$\mathbf{A} \mathbf{x} = \mathbf{b}$

係数行列 $\mathbf{A}$ は、その対角成分を取り出した行列 $\mathbf{D}$ 、対角と対角より下をゼロとした上三角の行列 $\mathbf{U}$ 、対角と対角より上をゼロとした下三角の行列 $\mathbf{L}$ より、 $\mathbf{A} = \mathbf{L} + \mathbf{D} + \mathbf{U}$ と表せるので、

$(\mathbf{L} + \mathbf{D} + \mathbf{U}) \mathbf{x} = \mathbf{b}$

$\mathbf{U} \mathbf{x}$ を右辺に移し、両辺に $(\mathbf{L} + \mathbf{D})^{-1}$ をかけると、

$\mathbf{x} = (\mathbf{L} + \mathbf{D})^{-1} (\mathbf{b} - \mathbf{U} \mathbf{x})$

逐次代入で数値解を得る形を考えると、

$\mathbf{x}^{(k+1)} = (\mathbf{L} + \mathbf{D})^{-1} (\mathbf{b} - \mathbf{U} \mathbf{x}^{(k)})$

Pythonを用いた解き方は例えば次のようになる。

import numpy as np

def gauss_seidel(A, b):
    x0 = np.zeros_like(b)  # xの初期値
    err = 1e10 # 収束判定用

    D = np.diag(A.diagonal())  # 係数行列Aの対角行列
    U = np.triu(A, k=1)  # 係数行列Aの対角を除く上三角の行列
    L = np.tril(A, k=-1)  # 係数行列Aの対角を除く下三角の行列
    invLD = np.linalg.inv(L + D)  # (L + D) の逆行列

    while err > 1e-5:
        x1 = np.dot(invLD, (b - np.dot(U, x0)))
        err = np.linalg.norm(b - np.dot(A, x1))/np.linalg.norm(b) # 収束判定
        x0 = x1

    return x0

A = np.array([[3, 1, -1],
              [-1, 2, 1],
              [1, -1, 2]])

b = np.array([2,
              6,
              5])

print(gauss_seidel(A, b))

解は $\mathbf{x}=[1, 2, 3$ ] であるが、上記コードの計算結果は下記でありよい近似値と言える。（なお上のコードは3x3の連立方程式に限らず、nxnについて適用できる。）

[0.9999933  1.99999866 3.00000268]

ガウス・ザイデル法はヤコビ法より早く計算が済む。収束判定条件を同じにしてヤコビ法とガウス・ザイデル法の計算時間を実際に比較してみると(Jupyter Notebook の %timeit で測定)、

ヤコビ法：

631 µs ± 1.57 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

ガウス・ザイデル法：

209 µs ± 725 ns per loop (mean ± std. dev. of 7 runs, 1000 loops each)

となり、この問題については実測としてガウス・ザイデル法のほうが3倍くらい早い結果となった。

2020-08-02

Pythonを用いた連立１次方程式の数値解法（ヤコビ法）

Python

はじめに

連立1次方程式の数値解を得るためのヤコビ法について、考え方とPythonを用いた計算のやり方を簡単に記す。

ヤコビ法

例えば次の連立方程式を考える。

これら方程式を次の近似解を得る形に書き直し、

解の最初の予測値を右辺に代入して計算し、得られた値を第2の予測値として再び右辺に代入して計算、を繰り返し近似解を得る数値解法がヤコビ法である。新しい解と1つ前の解の差が予め決めた許容値を下回るまで計算を繰り返す。

なおこれら近似式は行列の形で表すと以下のとおりとなる。まずはじめの方程式は

として、

$\mathbf{A} \mathbf{x} = \mathbf{b}$

係数行列 $\mathbf{A}$ は、その対角成分を取り出した行列 $\mathbf{D}$ と対角成分をゼロとした行列 $\mathbf{R}$ より、 $\mathbf{A} = \mathbf{D} + \mathbf{R}$ と表せるので、

$(\mathbf{D}+\mathbf{R}) \mathbf{x} = \mathbf{b}$

更に式変形していくと、次の形になる。

$\mathbf{x} = \mathbf{D}^{-1} (\mathbf{b} - \mathbf{R} \mathbf{x})$

逐次代入で数値解を得る形を考えると、

$\mathbf{x}^{(k+1)} = \mathbf{D}^{-1} (\mathbf{b} - \mathbf{R} \mathbf{x}^{(k)})$

これは、上述の3つ並べた近似式と同内容である。

Pythonを用いた解き方は例えば次のようになる。

import numpy as np

def jacobi(A, b):
    x0 = np.zeros_like(b)  # xの初期値
    err = 1e10  # 収束判定用

    D = np.diag(A.diagonal())  # 係数行列Aの対角成分を取り出した行列
    R = A - D  # 係数行列Aの対角成分を0にした行列
    invD = np.linalg.inv(D)  # Dの逆行列

    while err > 1e-5:
        x1 = np.dot(invD, (b - np.dot(R, x0)))
        err = np.linalg.norm(b - np.dot(A, x1))/np.linalg.norm(b)  # 収束判定
        x0 = x1

    return x0

A = np.array([[3, 1, -1],
              [-1, 2, 1],
              [1, -1, 2]])

b = np.array([2,
              6,
              5])

print(jacobi(A, b))

解は $\mathbf{x}=[1, 2, 3$ ] であるが、上記コードの計算結果は下記でありよい近似値と言える。

[0.99999306 2.00002081 2.99998959]

モデリングと数値計算（主に化学工学向け）

化学反応、移動現象のモデリングと数値計算の話

管内流れの1次元移流拡散方程式

はじめに

導出

差分近似による数値解法

計算例

管内の1次元拡散方程式

はじめに

導出

差分近似による数値解法

計算例

管内流れの1次元移流方程式

はじめに

導出

吸着平衡　ー平衡到達時の吸着量計算ー

はじめに

解き方

Pythonを用いた非線形方程式の数値解法　ニュートン法

はじめに

ニュートン法

Pythonを用いた連立１次方程式の数値解法（ガウス・ザイデル法）

はじめに

ガウス・ザイデル法

Pythonを用いた連立１次方程式の数値解法（ヤコビ法）

はじめに

ヤコビ法